競技プログラミングや実務におけるデータ分析において、配列内の特定の範囲の合計値を高速に求める手法は非常に重要です。

その中でも「累積和」は、シンプルながらも劇的なパフォーマンス向上をもたらす、最も基本的かつ強力なアルゴリズムの一つです。

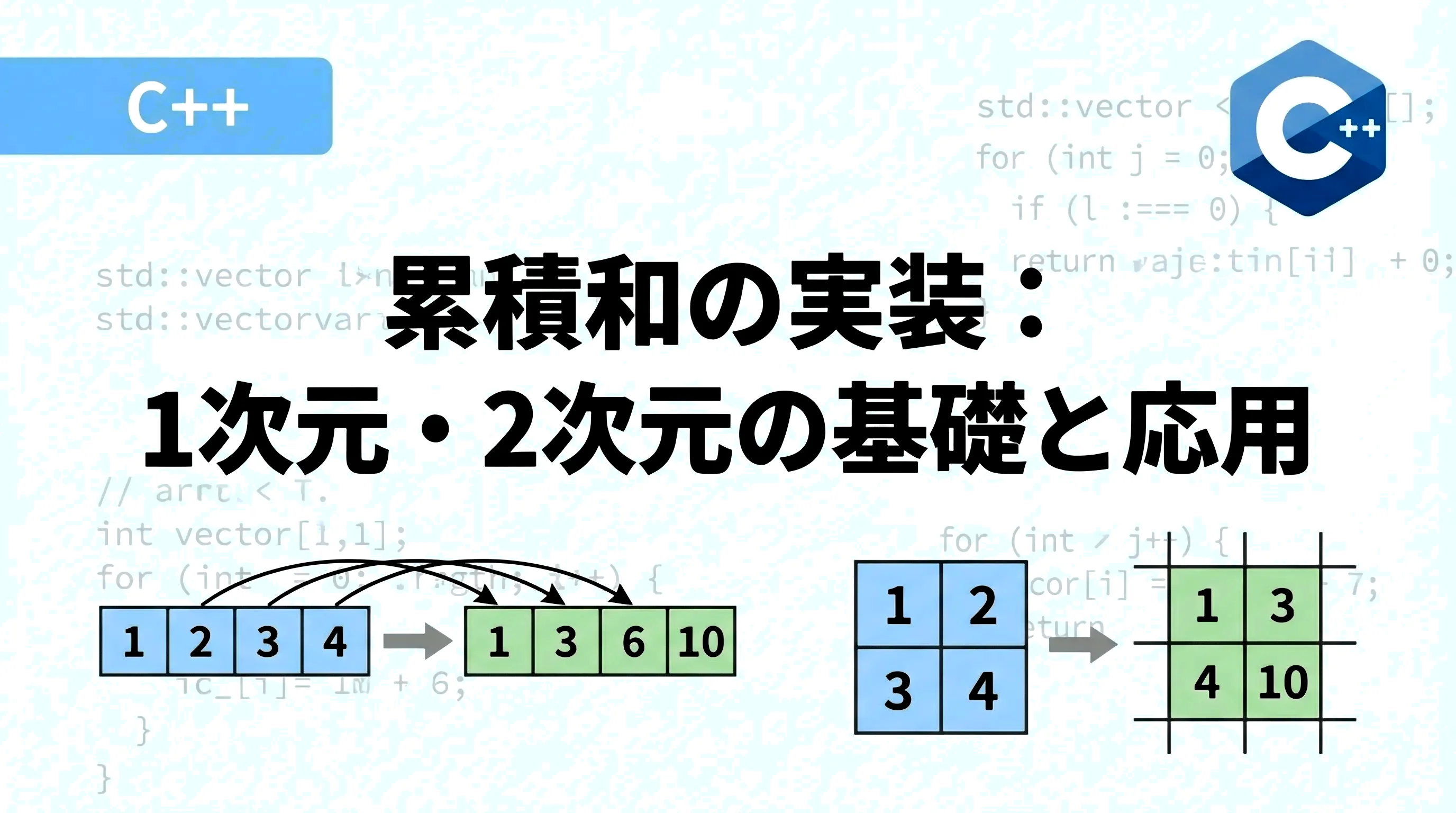
本記事では、C++を用いた累積和の実装方法について、基礎的な1次元から応用的な2次元、さらには関連するテクニックまでを詳しく解説します。

目次 [ close ]
  1. 累積和の基本概念と導入のメリット
  2. 1次元累積和のアルゴリズムと実装
    1. 構築の原理
    2. 区間和の算出
    3. C++による1次元累積和の実装例
  3. 2次元累積和のアルゴリズムと実装
    1. 構築の原理
    2. 矩形領域の和の算出
    3. C++による2次元累積和の実装例
  4. 累積和の応用：いもす法と差分配列
    1. 差分配列（Difference Array）の仕組み
    2. いもす法の実装例
  5. C++標準ライブラリの活用：std::partial_sum
    1. std::partial_sum の使用例
  6. 実装における注意点とトラブルシューティング
    1. 1. インデックスのオフセット
    2. 2. データ型の選択
    3. 3. 多次元への拡張
  7. 累積和をいつ使うべきか？（判別基準）
  8. まとめ

累積和の基本概念と導入のメリット

累積和（Cumulative Sum / Prefix Sum）とは、配列の先頭から各要素までの合計をあらかじめ計算しておく手法のことです。

この手法を導入する最大のメリットは、「任意の区間の和を $O(1)$ の計算量で求められる」という点にあります。

例えば、要素数 N の配列に対して、指定された範囲の合計を求めるクエリが Q 回投げられる状況を考えてみましょう。

毎回愚直にループを回して合計を算出する場合、1回あたりの計算量は最大で O(N) となり、全体では O(NQ) の時間がかかります。

N や Q が $10^5$ を超えるようなケースでは、この処理は制限時間内に終わりません。

しかし、累積和を事前に構築しておけば、構築に O(N)、各クエリへの応答に O(1) しかかからず、全体で O(N + Q) となり、計算量を劇的に削減することが可能です。

1次元累積和のアルゴリズムと実装

まずは最も基本的な1次元の累積和について見ていきましょう。

構築の原理

元の配列を A、累積和を格納する配列を S とします。

累積和配列 S の各要素は以下のように定義されます。

  • S[0] = 0
  • S[i+1] = S[i] + A[i] （$i = 0, 1, …, N-1$）

このように定義することで、S[i] は「元の配列の先頭から i 個の要素の合計」を表すことになります。

累積和配列のサイズは、元の配列のサイズよりも 1つ大きく確保するのが一般的です。

これにより、空の範囲（合計0）をスマートに扱うことができます。

区間和の算出

半開区間 [left, right)（left 番目から right-1 番目までの要素）の和を求めたい場合、累積和配列を使えば以下の計算式だけで完結します。

区間和 = S[right] – S[left]

これは、「先頭から right 個の和」から「先頭から left 個の和」を引くことで、目的の範囲の和が残るという理屈に基づいています。

C++による1次元累積和の実装例

以下のコードは、C++で1次元累積和を構築し、クエリに応答する基本的な実装です。

C++
#include <iostream>
#include <vector>
#include <numeric>

int main() {
    // 入力データの例
    int n = 6;
    std::vector<int> a = {3, 1, 4, 1, 5, 9};

    // 累積和配列の構築 (サイズは n+1)
    // s[i] は a[0] から a[i-1] までの和を格納する
    std::vector<long long> s(n + 1, 0);
    for (int i = 0; i < n; ++i) {
        s[i + 1] = s[i] + a[i];
    }

    // クエリの例: インデックス [2, 5) の範囲の和を求める
    // a[2]=4, a[3]=1, a[4]=5 の合計は 10 となるはず
    int left = 2;
    int right = 5;
    long long range_sum = s[right] - s[left];

    std::cout << "区間 [" << left << ", " << right << ") の和: " << range_sum << std::endl;

    // 全要素の累積和配列を表示
    std::cout << "累積和配列 s: ";
    for (long long x : s) {
        std::cout << x << " ";
    }
    std::cout << std::endl;

    return 0;
}
実行結果
区間 [2, 5) の和: 10
累積和配列 s: 0 3 4 8 9 14 23

この実装では、和が大きくなる可能性を考慮して long long 型を使用しています。

整数のオーバーフローは累積和を扱う際によくあるミスの一つですので、常に意識しておく必要があります。

2次元累積和のアルゴリズムと実装

1次元の考え方を拡張することで、行列などの2次元平面における矩形領域の和も高速に計算できるようになります。

構築の原理

2次元累積和配列 S[i][j] を、「元の2次元配列 A の左上（0,0）から座標（i-1, j-1）までの矩形領域の総和」と定義します。

この構築には「包除原理」に似た考え方を用います。

S[i][j] を計算する際、以下の漸化式を利用します。

S[i][j] = S[i-1][j] + S[i][j-1] – S[i-1][j-1] + A[i-1][j-1]

  • S[i-1][j]: 1行上の領域の和
  • S[i][j-1]: 1列左の領域の和
  • S[i-1][j-1]: 重複して足された左上の領域を引く
  • A[i-1][j-1]: 現在の要素を足す

矩形領域の和の算出

任意の矩形領域（行が r1 から r2-1、列が c1 から c2-1）の和を求めたい場合、累積和配列を使って以下のように計算します。

領域和 = S[r2][c2] – S[r1][c2] – S[r2][c1] + S[r1][c1]

この式も包除原理に基づいています。

全体の矩形から「上の矩形」と「左の矩形」を引き、引きすぎてしまった「左上の矩形」を戻すことで、目的の領域だけの和が算出されます。

C++による2次元累積和の実装例

2次元累積和は多重ループを用いて構築します。

インデックスの扱いに注意しながら実装を進めます。

C++
#include <iostream>
#include <vector>

int main() {
    // 3x3 の2次元配列の例
    int h = 3, w = 3;
    std::vector<std::vector<int>> a = {
        {1, 2, 3},
        {4, 5, 6},
        {7, 8, 9}
    };

    // 累積和配列の構築 (サイズは (h+1) x (w+1))
    std::vector<std::vector<long long>> s(h + 1, std::vector<long long>(w + 1, 0));

    for (int i = 0; i < h; ++i) {
        for (int j = 0; j < w; ++j) {
            s[i + 1][j + 1] = s[i][j + 1] + s[i + 1][j] - s[i][j] + a[i][j];
        }
    }

    // 矩形領域 [(1,1) から (3,3)) の和を求める
    // つまり a[1][1], a[1][2], a[2][1], a[2][2] の合計
    // 5 + 6 + 8 + 9 = 28 となるはず
    int r1 = 1, c1 = 1, r2 = 3, c2 = 3;
    long long rect_sum = s[r2][c2] - s[r1][c2] - s[r2][c1] + s[r1][c1];

    std::cout << "矩形領域の和: " << rect_sum << std::endl;

    // 累積和配列の表示
    std::cout << "2次元累積和配列 s:" << std::endl;
    for (int i = 0; i <= h; ++i) {
        for (int j = 0; j <= w; ++j) {
            std::cout << s[i][j] << "\t";
        }
        std::cout << std::endl;
    }

    return 0;
}
実行結果
矩形領域の和: 28
2次元累積和配列 s:
0	0	0	0	
0	1	3	6	
0	5	12	21	
0	12	27	45

2次元累積和の構築も O(HW) で完了し、クエリ応答は O(1) です。

画像処理における移動平均フィルタ（ボックスフィルタ）や、2次元マップ上の集計などで非常に強力なツールとなります。

累積和の応用：いもす法と差分配列

累積和の考え方を「逆」に利用することで、「区間全体に値を加算する」という操作を高速化できます。

これがいわゆる「いもす法（IMOS Method）」や「差分配列」と呼ばれるテクニックです。

差分配列（Difference Array）の仕組み

長さ N の配列に対して、「インデックス l から r-1 までのすべての要素に v を足す」というクエリが大量にある場合を想定します。

愚直に行うと1クエリ O(N) ですが、差分配列 D を用意し、以下の2点だけの更新に留めることで O(1) に短縮できます。

  1. D[l] += v
  2. D[r] -= v

すべてのクエリが終わった後に、この差分配列 D に対して累積和をとることで、最終的な各要素の値を一挙に得ることができます。

いもす法の実装例

以下のコードは、複数の区間加算クエリを処理し、最終的な配列の状態を出力する例です。

C++
#include <iostream>
#include <vector>

int main() {
    int n = 10; // 配列のサイズ
    std::vector<int> diff(n + 1, 0); // 差分配列

    // クエリ1: [2, 5) に +3
    diff[2] += 3;
    diff[5] -= 3;

    // クエリ2: [4, 8) に +2
    diff[4] += 2;
    diff[8] -= 2;

    // 累積和をとって結果を復元
    std::vector<int> result(n, 0);
    int current_sum = 0;
    for (int i = 0; i < n; ++i) {
        current_sum += diff[i];
        result[i] = current_sum;
    }

    std::cout << "最終的な配列の状態: ";
    for (int x : result) {
        std::cout << x << " ";
    }
    std::cout << std::endl;

    return 0;
}
実行結果
最終的な配列の状態: 0 0 3 3 5 2 2 2 0 0

このように、加算操作が累積和の構築前に集中している場合、いもす法は極めて有効です。

なお、加算と取得が交互に行われるような動的なケースでは、「Binary Indexed Tree (BIT)」や「セグメント木」といったデータ構造が必要になります。

C++標準ライブラリの活用：std::partial_sum

C++には、累積和を計算するための標準アルゴリズム std::partial_sum が <numeric> ヘッダに用意されています。

自前でループを書くよりも簡潔に記述でき、ミスを減らすことができます。

std::partial_sum の使用例

C++
#include <iostream>
#include <vector>
#include <numeric> // std::partial_sum
#include <iterator>

int main() {
    std::vector<int> a = {1, 2, 3, 4, 5};
    std::vector<int> s(a.size());

    // a の累積和を s に格納
    std::partial_sum(a.begin(), a.end(), s.begin());

    std::cout << "std::partial_sum による結果: ";
    for (int x : s) {
        std::cout << x << " ";
    }
    std::cout << std::endl;

    return 0;
}

ただし、競技プログラミングなどでよく使われる「サイズを1つ大きくして先頭を0にする」というスタイルで構築したい場合は、手動でループを書くか、代入先を調整する工夫が必要です。

実装における注意点とトラブルシューティング

累積和を実装する際に陥りやすい罠がいくつか存在します。

1. インデックスのオフセット

累積和配列を元のサイズ N で作るか、N+1 で作るかは常に議論の的になりますが、基本的には N+1 で作ることを推奨します。

  • S[0] = 0 とすることで、区間 [0, r) の和を求める際も S[r] - S[0] という統一された式で記述できます。
  • サイズ N で作ってしまうと、left=0 の場合に条件分岐が必要になり、コードの可読性が下がりバグの原因となります。

2. データ型の選択

累積和は値を足し合わせるため、元の配列の要素が小さくても合計値は非常に大きくなることがあります。

要素の最大値要素数 (N)最大合計値推奨型
$10^5$$10^5$$10^{10}$long long
$10^9$$10^6$$10^{15}$long long
$10$$10^2$$10^3$int

C++の int 型は約 $2 \times 10^9$ までしか保持できません。

$10^5$ 程度の要素数であっても、各要素が $10^5$ ならば合計は $10^{10}$ となり、int を超えます。

原則として 累積和配列には long long を使用するのが安全です。

3. 多次元への拡張

本記事では2次元までを解説しましたが、3次元、4次元と拡張することも理論上可能です。

しかし、次元が増えるごとに包除原理の項数が $2^d$ のオーダーで増加するため、実装が複雑になります。

高次元の累積和が必要な場合は、1次元ずつの累積和を各軸に対して順番に適用していく手法をとると、実装がシンプルになります。

累積和をいつ使うべきか？（判別基準）

「この問題に累積和が使えるか？」を判断する基準は以下の通りです。

  • 静的な配列に対する区間集計: 配列の内容が途中で更新されない。
  • 結合則を満たす演算: 和以外にも、積（逆元がある場合）や XOR 演算などは累積和の考え方が適用できます。
  • 逆演算が可能:区間和を引くことで求められるのは、足し算に対して引き算という逆演算が存在するからです。
    ※Max や Min は逆演算ができないため、通常の累積和では区間最大値を求めることはできません（その場合はセグメント木や Sparse Table を検討します）。

まとめ

累積和は、計算量を劇的に改善するための「初手」として非常に重要なアルゴリズムです。

  • 1次元累積和は、事前準備 $O(N)$ で任意の区間和を $O(1)$ にします。
  • 2次元累積和は、包除原理を利用して矩形領域の和を $O(1)$ にします。
  • いもす法は、累積和の逆の操作で区間加算を高速化します。
  • 実装時は配列サイズを N+1 にすることと、オーバーフロー（long long の使用）に注意してください。

C++の強力な型システムと標準ライブラリを活かしつつ、これらのテクニックを自在に使いこなせるようになれば、アルゴリズムの実装力は一段上のレベルへと到達するでしょう。

まずは手元のエディタで、簡単な配列に対して累積和を構築する練習から始めてみてください。