C++を用いた数値計算やアルゴリズムの実装において、値の絶対値を求める処理は非常に頻繁に登場します。

距離の計算、誤差の評価、物理シミュレーションなど、負の値を考慮せずに「大きさ」だけを抽出したい場面は多岐にわたります。

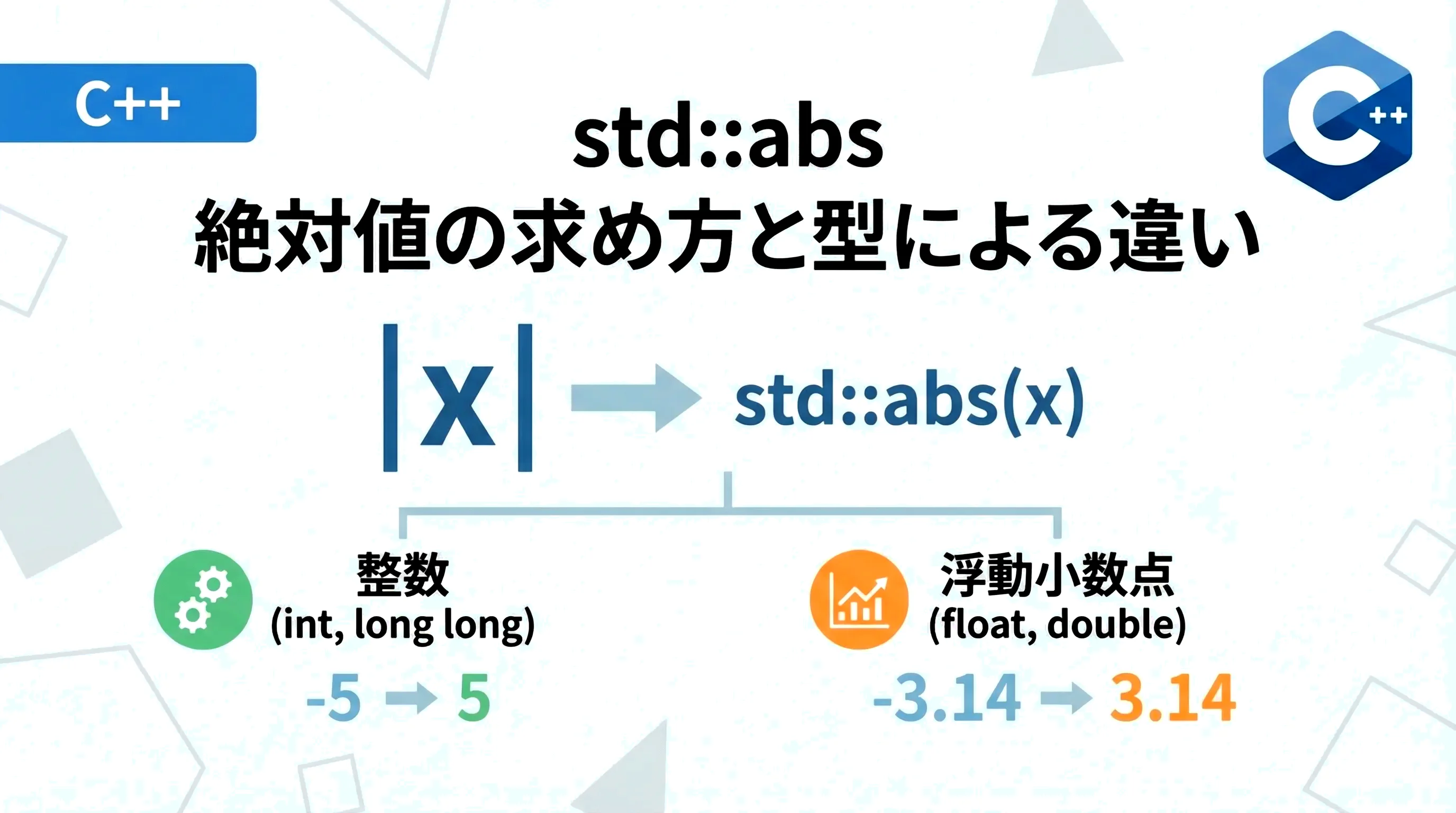
C++では、標準ライブラリが提供するstd::abs関数を使用することで、整数型から浮動小数点型、さらには複素数まで、多様な型の絶対値を一貫したインターフェースで取得することが可能です。

本記事では、C++における絶対値計算の基本から、型による挙動の違い、さらには符号付き整数における注意点や最新のC++規格における変更点まで、プロフェッショナルな視点で詳しく解説します。

目次 [ close ]
  1. C++における絶対値計算の基本：std::absとは
    1. 必要なヘッダーファイル
    2. 基本的な使用例
  2. 整数型におけるstd::absの挙動と注意点
    1. 対応している整数型
    2. 負の最大値（INT_MIN）によるオーバーフロー
  3. 浮動小数点型におけるstd::absの挙動
    1. 精度に応じた適切なオーバーロード
    2. 特別な値（NaN, Infinity）の扱い
  4. C関数（abs, fabs等）とC++のstd::absの違い
    1. C言語の絶対値関数の制限
    2. なぜstd::absを使うべきか
  5. 複素数に対するstd::abs
  6. モダンC++におけるstd::abs：constexpr対応
  7. ジェネリックなコードでの活用：テンプレートとstd::abs
  8. パフォーマンスと最適化の観点
  9. 符号なし整数（unsigned）にstd::absを使うとどうなるか
  10. まとめ

C++における絶対値計算の基本：std::absとは

C++で絶対値を求めるための最も標準的かつ推奨される方法は、std::abs関数を使用することです。

この関数は、引数として与えられた数値が負であればその符号を反転させ、正またはゼロであればそのままの値を返します。

C++のstd::absは、C言語から引き継いだ機能に加えて、C++独自の関数オーバーロードという仕組みを利用して拡張されています。

これにより、プログラマは引数の型が何であるかを過度に意識することなく、同じ関数名で適切な処理を呼び出すことができます。

必要なヘッダーファイル

C++でstd::absを使用する場合、主に2つのヘッダーファイルが関係します。

  1. <cmath>：浮動小数点型（float, double, long double）および整数型に対するオーバーロードが定義されています。
  2. <cstdlib>：主に整数型（int, long, long long）に対する絶対値関数が定義されています。

現代的なC++開発においては、数値計算を扱う場合は<cmath>をインクルードするのが一般的です。

<cmath>をインクルードすることで、整数と浮動小数点型の両方に対して一貫したstd::absのオーバーロードを利用できるため、コードの可搬性と保守性が向上します。

基本的な使用例

以下のコードは、整数と浮動小数点数に対してstd::absを適用するもっともシンプルな例です。

C++
#include <iostream>
#include <cmath> // std::absを使用するために必要

int main() {
    int n = -10;
    double d = -25.5;

    // 整数型の絶対値
    int abs_n = std::abs(n);
    // 浮動小数点型の絶対値
    double abs_d = std::abs(d);

    std::cout << "Integer: " << n << " -> " << abs_n << std::endl;
    std::cout << "Double: " << d << " -> " << abs_d << std::endl;

    return 0;
}
実行結果
Integer: -10 -> 10
Double: -25.5 -> 25.5

整数型におけるstd::absの挙動と注意点

整数型に対する絶対値計算は単純に見えますが、計算機科学の観点からはいくつかの重要な制約が存在します。

特に、符号付き整数の内部表現である2の補数形式に起因する問題には注意が必要です。

対応している整数型

C++標準ライブラリでは、以下の整数型に対してstd::absがオーバーロードされています。

型説明
int標準的な符号付き整数型
long少なくとも32ビット以上の符号付き整数型
long long少なくとも64ビット以上の符号付き整数型

これらより小さい型（shortやsigned charなど）が引数として渡された場合、通常はint型に整数昇格された上で処理されます。

負の最大値（INT_MIN）によるオーバーフロー

整数型で最も注意すべき点は、型の最小値（負の最大値）を絶対値に変換しようとすると未定義動作（Undefined Behavior）を引き起こす可能性があるという点です。

例えば、多くの環境で32ビット整数（int）の範囲は -2,147,483,648 から 2,147,483,647 です。

ここで、-2,147,483,648 の絶対値は 2,147,483,648 ですが、これは int 型の最大値を超えています。

C++
#include <iostream>
#include <cmath>
#include <climits> // INT_MINを使用するために必要

int main() {
    int min_val = INT_MIN;
    
    // INT_MINの絶対値はintの最大値を超えるため、未定義動作となる可能性がある
    // 実際の結果は環境に依存する（多くの場合、元の負の値に戻るか、そのまま出力される）
    int result = std::abs(min_val);

    std::cout << "INT_MIN: " << min_val << std::endl;
    std::cout << "abs(INT_MIN): " << result << std::endl;

    return 0;
}

実行結果（一例）：

実行結果
INT_MIN: -2147483648
abs(INT_MIN): -2147483648

このように、結果が元の負の数値のままになってしまう現象が発生します。

これを防ぐためには、計算前に範囲チェックを行うか、より大きな型（long longなど）へキャストしてから計算する、あるいはC++20以降であれば数学的特性を考慮した実装を検討する必要があります。

浮動小数点型におけるstd::absの挙動

浮動小数点型（float, double, long double）における絶対値計算は、std::absが提供する最も強力な機能の一つです。

精度に応じた適切なオーバーロード

<cmath>ヘッダーでは、引数の精度に合わせて最適な戻り値を返すように定義されています。

  • float std::abs(float arg);
  • double std::abs(double arg);
  • long double std::abs(long double arg);

これにより、double型の値を渡したのに、誤って精度の低いintとして計算されて小数点以下が切り捨てられる、といった事故を防ぐことができます。

特別な値（NaN, Infinity）の扱い

浮動小数点数には、非数（NaN）や無限大（Infinity）といった特別な状態が存在します。

C++のstd::absは、IEEE 754規格に準拠した環境において、これらを適切に処理します。

  • Infinity：正の無限大（+Inf）および負の無限大（-Inf）の絶対値は、ともに正の無限大となります。
  • NaN：引数がNaNである場合、結果もNaNとなります。
  • 負のゼロ：-0.0の絶対値は、通常の0.0になります。
C++
#include <iostream>
#include <cmath>
#include <limits>

int main() {
    double inf = std::numeric_limits<double>::infinity();
    double neg_inf = -inf;
    double nan = std::numeric_limits<double>::quiet_NaN();

    std::cout << "abs(-Inf) = " << std::abs(neg_inf) << std::endl;
    std::cout << "abs(NaN)  = " << std::abs(nan) << std::endl;
    std::cout << "abs(-0.0) = " << std::abs(-0.0) << std::endl;

    return 0;
}
実行結果
abs(-Inf) = inf
abs(NaN)  = nan
abs(-0.0) = 0

C関数（abs, fabs等）とC++のstd::absの違い

C++はC言語との互換性を持っているため、C由来の絶対値関数も利用可能です。

しかし、C++の開発においては、これらを直接呼び出すよりもstd::absを使用することが推奨されます。

C言語の絶対値関数の制限

C言語では関数名のオーバーロードが許可されていないため、型ごとに異なる関数名を使用しなければなりませんでした。

関数名対象となる型
absint
labslong
llabslong long
fabsdouble
fabsffloat
fabsllong double

C++においてこれらの古い関数を使用すると、型の不一致によるバグの原因になります。

例えば、abs(-2.5) と記述した場合、C言語の abs(int) が選ばれてしまうと、戻り値が整数値の 2 になり、小数点以下が失われます。

一方、C++のstd::abs(-2.5)であれば、適切に浮動小数点数用のオーバーロードが選択され、2.5 が返されます。

なぜstd::absを使うべきか

  1. 型の安全性：コンパイラが引数の型に応じて最適な関数を自動選択します。
  2. テンプレートとの親和性：ジェネリックなコード（関数テンプレートなど）を書く際、型を意識せず std::abs(t) と書くだけで動作します。
  3. 標準規格への準拠：C++の標準規格は、浮動小数点数に対しても std::abs を使うことを正式な作法としています。

複素数に対するstd::abs

C++のstd::absは、<complex>ヘッダーをインクルードすることで、複素数型（std::complex）に対しても動作するようになります。

複素数に対する絶対値は、数学的には複素数平面上の原点からの距離（絶対値、ノルム）を意味します。

式で表すと、実部を $a$、虚部を $b$ としたとき、 $\sqrt{a^2 + b^2}$ となります。

C++
#include <iostream>
#include <complex>
#include <cmath>

int main() {
    std::complex<double> z(3.0, 4.0); // 3 + 4i

    // 複素数の絶対値（√(3^2 + 4^2) = √25 = 5）
    double magnitude = std::abs(z);

    std::cout << "Complex number: " << z << std::endl;
    std::cout << "Magnitude: " << magnitude << std::endl;

    return 0;
}
実行結果
Complex number: (3,4)
Magnitude: 5

複素数の場合、戻り値は「複素数」ではなく、その大きさを表す「実数（浮動小数点数）」になることに注意してください。

モダンC++におけるstd::abs：constexpr対応

最新のC++（C++20以降）では、std::absの多くがconstexprに対応しています。

これにより、コンパイル時に絶対値計算を行うことが可能になり、実行時のパフォーマンス向上や、テンプレート引数などの定数式が必要な場面での利用が容易になりました。

C++
#include <iostream>
#include <cmath>

int main() {
    // コンパイル時に絶対値が計算される
    constexpr int abs_val = std::abs(-42);
    constexpr double abs_double = std::abs(-3.14);

    static_assert(abs_val == 42, "Check failed!");
    
    std::cout << "Compile-time absolute values verified." << std::endl;
    return 0;
}

static_assertを使用してコンパイル時にチェックができることは、ライブラリ開発や組み込みシステムなどの制約が厳しい環境において非常に強力な武器となります。

ジェネリックなコードでの活用：テンプレートとstd::abs

関数テンプレートを作成する際、引数が整数なのか浮動小数点数なのか不明な場合があります。

このような場合でも、std::absは柔軟に対応可能です。

ただし、名前空間の扱いには一つのテクニックがあります。

それは「ADL（Argument Dependent Lookup：引数依存名前空間探索）」を利用する方法です。

C++
#include <iostream>
#include <cmath>
#include <complex>

template <typename T>
void print_absolute_value(T val) {
    using std::abs; // std::absを使えるようにする
    std::cout << "The absolute value is: " << abs(val) << std::endl;
}

int main() {
    print_absolute_value(-10);        // int
    print_absolute_value(-5.5);       // double
    print_absolute_value(std::complex<double>(1.0, 1.0)); // complex
    return 0;
}

このように using std::abs; と記述してから abs(val) と呼び出すことで、標準型には std::abs が適用され、ユーザー定義型（独自の複素数クラスなど）にはその型と同じ名前空間で定義された abs 関数が優先的に適用されるようになります。

これはC++において非常に堅牢な設計パターンとされています。

パフォーマンスと最適化の観点

絶対値計算は、内部的には「符号ビットのクリア」や「条件分岐による反転」として実装されます。

現代のコンパイラは std::abs を非常に高度に最適化します。

  1. インライン展開：関数呼び出しのオーバーヘッドはなく、直接的な機械語命令（x86の PABS 命令や浮動小数点の FABS 等）に置換されます。
  2. 分岐予測：整数絶対値の場合、ビット演算を用いて条件分岐なし（Branchless）で実装されることが多く、パイプラインの乱れを防ぎます。

したがって、自分で val < 0 ? -val : val といったコードを書くよりも、std::absに任せる方が、読みやすく、かつ最速のコードになる可能性が高いと言えます。

符号なし整数（unsigned）にstd::absを使うとどうなるか

意外な落とし穴として、符号なし整数型（unsigned int等）をstd::absに渡すことが挙げられます。

数学的には「符号なし整数の絶対値はその値自身」ですが、C++のオーバーロード解決において、符号なし整数を std::abs に渡すと、コンパイルエラーになるか、あるいは意図しない型変換が行われることがあります。

C++
unsigned int u = 10;
// 警告やエラーの原因になる可能性がある
// また、符号なしなのでそもそも絶対値をとる意味がない
auto result = std::abs(u);

C++23以降、符号なし整数に対する std::abs は、単にその値をそのまま返すように規定されていますが、コードの意図を明確にするためにも、符号なし整数に対して絶対値関数を呼び出すのは避けるべきです。

もし差分を計算したい場合は、std::max と std::min を組み合わせて max(a, b) - min(a, b) とするか、C++20の std::abs_diff （将来的な検討候補）のような概念を意識する必要があります。

まとめ

C++において絶対値を求めるstd::absは、単純な関数に見えて非常に奥が深く、言語の進化と共に洗練されてきた機能です。

  • ヘッダーは<cmath>を使用することで、整数と浮動小数点の両方に対応できる。
  • 型安全であり、C言語の fabs や labs を個別に使い分ける必要はない。
  • 符号付き整数の最小値（INT_MIN）ではオーバーフローが発生し、未定義動作となるリスクがある。
  • 複素数に対しても、その大きさを計算する手段として一貫したインターフェースを提供する。
  • Modern C++では constexpr 対応が進んでおり、コンパイル時計算が可能である。

これらの特性を理解し、適切に使い分けることで、バグが少なく効率的な数値計算プログラムを記述することができます。

特にC言語出身のエンジニアは、fabs などの型限定の関数から、より汎用的な std::abs へと移行することをお勧めします。