C++において乱数生成は、ゲーム開発、統計シミュレーション、暗号化、テストデータの作成など、多岐にわたる分野で不可欠な要素です。
かつてのC++ではC言語由来のrand()関数が広く使われてきましたが、現代のC++(C++11以降)では<random>ヘッダーに定義された新しいライブラリの使用が標準となっています。
従来のrand()には、精度の低さや分布の偏りといった多くの課題がありましたが、現代的なアプローチを採用することで、より安全で高品質な乱数生成が可能になります。
本記事では、C++における正しい乱数生成の仕組みと、推奨される実装例について詳しく解説します。
なぜ従来のrand()を使用してはいけないのか
C++11より前の時代に標準だったrand()関数とsrand()関数の組み合わせは、現代のソフトウェア開発においては非推奨とされています。
その理由は主に3つあります。
1. 乱数の質と周期の短さ
多くの標準ライブラリの実装において、rand()は「線形合同法」という単純なアルゴリズムを使用しています。
この手法は計算負荷が低い一方で、生成される数値の周期が短く、大規模なシミュレーションなどでは同じパターンがすぐに繰り返されてしまう欠点があります。
2. 剰余演算による分布の偏り
特定の範囲の乱数を得るためにrand() % nというコードがよく書かれますが、これは統計的な偏り(モジュロバイアス)を引き起こします。
例えば、rand()の最大値が32767で、0から9までの乱数を得たい場合、各数値の出現確率は完全には均等になりません。
3. グローバルな状態管理
rand()は内部でグローバルな状態(シード値)を保持しているため、マルチスレッド環境での安全性が保障されません。
複数のスレッドから同時にアクセスすると、予期しない動作やパフォーマンスの低下を招く可能性があります。
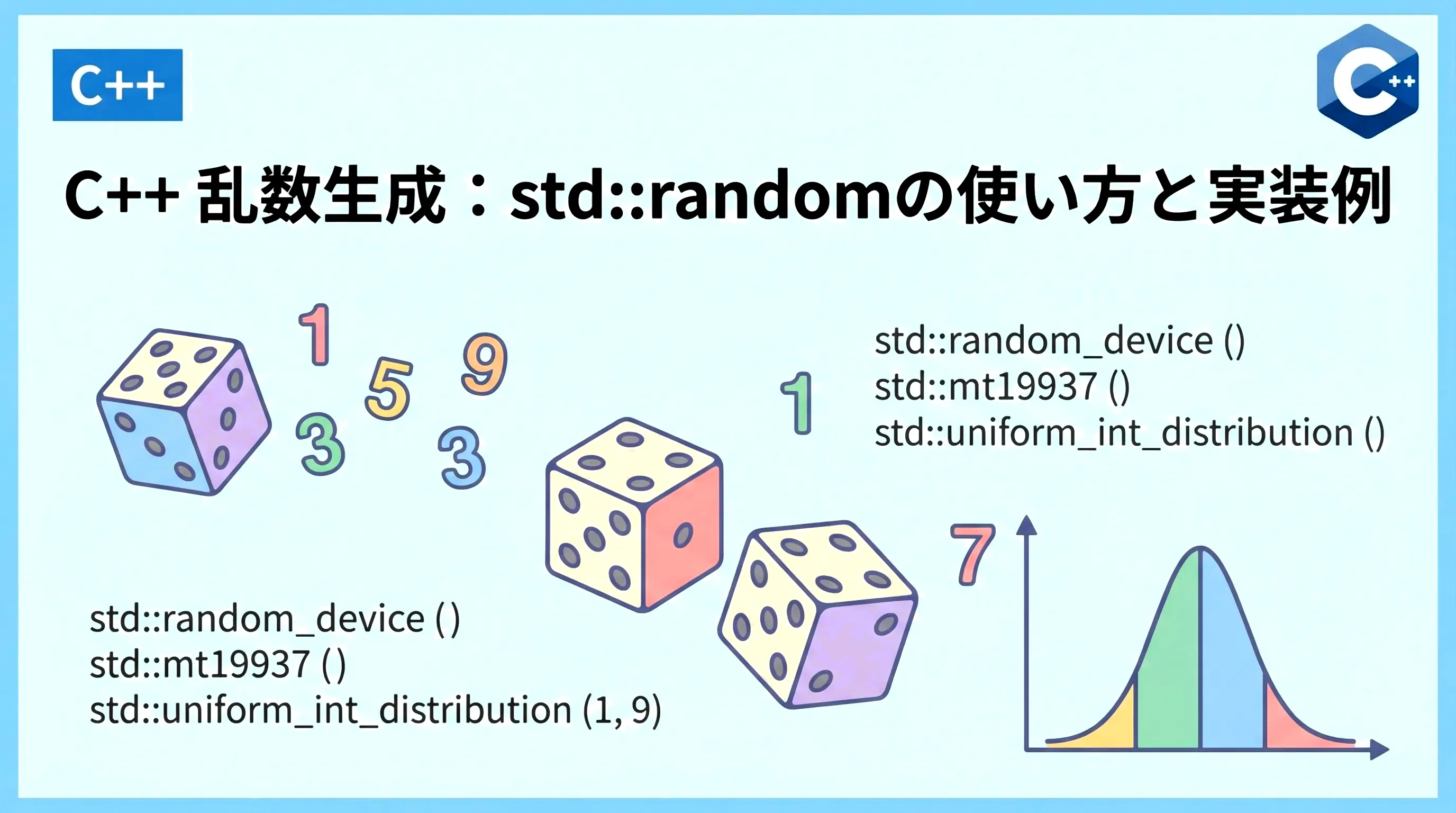
C++ <random> ライブラリの基本構成
C++11で導入された<random>ライブラリは、乱数生成のプロセスを「シード(種)」、「エンジン(生成機)」、「分布(分布器)」の3つの役割に分離しています。
この設計により、柔軟性が高く、かつ予測可能な動作を実現しています。
| コンポーネント | 役割 | 主なクラス |
|---|---|---|
| シード生成器 | エンジンを初期化するための真の乱数、または非決定的な値を提供 | std::random_device |
| 乱数生成エンジン | アルゴリズムに基づき、ビット列としての乱数シーケンスを生成 | std::mt19937 (メルセンヌ・ツイスタ) |
| 乱数分布器 | エンジンが生成した数値を、指定した範囲や確率分布に変換 | std::uniform_int_distribution など |
このように役割を分担することで、「どのアルゴリズムを使って(エンジン)」、「どのような範囲で(分布)」乱数を得るかを明確に定義できます。
推奨される乱数生成の標準的な実装例
現代のC++において最も推奨されるのは、メルセンヌ・ツイスタ(std::mt19937)をエンジンとして使用する方法です。
このアルゴリズムは非常に長い周期(2の19937乗-1)を持ち、統計的な性質も極めて優れています。
以下に、整数の乱数を生成する標準的なプログラムを示します。
#include <iostream>
#include <random> // 乱数ライブラリ
int main() {
// 1. 非決定的な乱数生成器(シード値用)
std::random_device seed_gen;
// 2. メルセンヌ・ツイスタエンジンをシード値で初期化
std::mt19937 engine(seed_gen());
// 3. 0から100までの範囲の整数を一様に分布させる分布器
// [0, 100] の範囲(100を含む)
std::uniform_int_distribution<int> dist(0, 100);
std::cout << "0から100までの乱数を5回生成します:" << std::endl;
for (int i = 0; i < 5; ++i) {
// エンジンを分布器に渡して乱数を取得
int result = dist(engine);
std::cout << result << std::endl;
}
return 0;
}0から100までの乱数を5回生成します:
42
18
89
7
53コードの解説
この例では、まずstd::random_deviceを使用して、ハードウェア由来のノイズなどから得られる真の乱数に近いシード値を取得しています。
これをstd::mt19937のコンストラクタに渡すことで、プログラムを実行するたびに異なる乱数系列が生成されるようになります。
その後、std::uniform_int_distributionを用いて、生成された巨大なビット列を特定の範囲(0~100)に数学的に正しくマッピングしています。
これにより、rand() % nで発生していた偏りの問題を完全に回避できます。
さまざまな分布クラスの活用
<random>ライブラリの強力な点は、用途に応じた多彩な分布クラスが用意されていることです。
1. 実数(浮動小数点数)の乱数
0.0から1.0までの範囲の小数を得るには、std::uniform_real_distributionを使用します。
#include <iostream>
#include <random>
#include <iomanip>
int main() {
std::random_device seed_gen;
std::mt19937 engine(seed_gen());
// 0.0以上 1.0未満の範囲の実数
std::uniform_real_distribution<double> dist(0.0, 1.0);
std::cout << std::fixed << std::setprecision(4);
for (int i = 0; i < 3; ++i) {
std::cout << dist(engine) << std::endl;
}
return 0;
}0.1245
0.8762
0.45312. 正規分布(ガウス分布)
平均値付近のデータが多く、平均から離れるほど少なくなるといった自然界の現象をシミュレートするにはstd::normal_distributionが便利です。
#include <iostream>
#include <random>
int main() {
std::random_device seed_gen;
std::mt19937 engine(seed_gen());
// 平均 50.0, 標準偏差 10.0 の正規分布
std::normal_distribution<double> dist(50.0, 10.0);
for (int i = 0; i < 3; ++i) {
std::cout << dist(engine) << std::endl;
}
return 0;
}48.2154
62.8791
51.04323. ベルヌーイ分布
「成功(true)」か「失敗(false)」を特定の確率で得たい場合は、std::bernoulli_distributionを使用します。
#include <iostream>
#include <random>
int main() {
std::random_device seed_gen;
std::mt19937 engine(seed_gen());
// 25%の確率で true を返す
std::bernoulli_distribution dist(0.25);
int true_count = 0;
for (int i = 0; i < 1000; ++i) {
if (dist(engine)) true_count++;
}
std::cout << "1000回中 true が出た回数: " << true_count << std::endl;
return 0;
}1000回中 true が出た回数: 248パフォーマンスと実装上の注意点
乱数生成を効率的に行うためには、いくつか避けるべきアンチパターンと推奨される手法があります。
エンジンをループ内で初期化しない
最も多い間違いは、乱数が必要になるたびにエンジン(std::mt19937)をローカル変数として再生成することです。
// 悪い例
for (int i = 0; i < 1000; ++i) {
std::random_device rd;
std::mt19937 engine(rd()); // ループのたびに初期化(非常に重い)
std::uniform_int_distribution<int> dist(1, 6);
process(dist(engine));
}メルセンヌ・ツイスタの初期化には比較的大きなコストがかかります。
また、非常に高速なループ内でtime(nullptr)などをシードにしている場合、同じシード値が何度も使われ、全て同じ乱数結果になるというバグの原因にもなります。
staticキーワードやクラスメンバの活用
エンジンは一度だけ初期化し、それを使い回すのが基本です。
関数内で使用する場合はstatic変数にするか、クラスのメンバ変数として保持することを検討してください。
int get_random_value() {
// 最初の呼び出し時にのみ初期化される
static std::random_device seed_gen;
static std::mt19937 engine(seed_gen());
std::uniform_int_distribution<int> dist(1, 100);
return dist(engine);
}マルチスレッド環境での注意
std::mt19937自体はスレッドセーフではありません。
マルチスレッド環境で並列に乱数を生成する場合、スレッドごとにエンジンを保持するthread_local修飾子の使用が効果的です。
thread_local std::mt19937 engine(std::random_device{}());これにより、ロック(mutex)によるオーバーヘッドを避けつつ、安全に高速な乱数生成が可能になります。
64ビット環境での乱数生成
現代のコンピューティング環境では64ビットの乱数が必要になる場面も多いでしょう。
その場合は、std::mt19937_64を使用します。
#include <iostream>
#include <random>
#include <cstdint>
int main() {
std::random_device seed_gen;
// 64ビット版メルセンヌ・ツイスタ
std::mt19937_64 engine(seed_gen());
// 広い範囲の64ビット整数
std::uniform_int_distribution<uint64_t> dist(0, 0xFFFFFFFFFFFFFFFF);
std::cout << "64ビット乱数: " << dist(engine) << std::endl;
return 0;
}64ビット乱数: 14757395258967641292std::mt19937は32ビットの値を生成するのに対し、std::mt19937_64は64ビットの内部状態を持ち、より広範囲な数値を一度に生成できます。
64ビットOS上でのシミュレーションやハッシュ計算用シードの生成にはこちらが適しています。
決定的な乱数が必要なケース
デバッグや単体テストにおいて、「常に同じ乱数系列」を得たい場合があります。
その場合は、std::random_deviceを使わずに固定の数値をシードとして渡します。
// 常に同じ結果が得られる
std::mt19937 engine(12345); // 固定のシード値このようにシード値を固定することで、バグの再現性を確保したり、特定の条件下での動作を検証したりすることが容易になります。
まとめ
現代のC++における乱数生成は、従来のrand()から<random>ライブラリへと完全に移行しました。
std::mt19937をはじめとする強力なエンジンと、目的に応じた多彩な分布クラスを組み合わせることで、統計的に正確で高品質な乱数を簡単に利用できます。
実装の際には、エンジンの初期化コストを意識し、不必要に再生成を行わないようにすることが重要です。
また、マルチスレッド環境や64ビット環境といった動作環境に合わせて適切なエンジン(thread_localやstd::mt19937_64)を選択するスキルも求められます。
本記事で紹介した手法を基本テンプレートとして活用し、安全で効率的なC++プログラミングを実践してください。
乱数の正しい理解と実装は、アプリケーションの信頼性と品質を大きく向上させる第一歩となります。