C++を用いた数値計算やアプリケーション開発において、浮動小数点数（double型やfloat型）の端数を処理する「切り捨て」は非常に頻繁に登場する操作です。

しかし、一口に切り捨てと言っても、負の値をどのように扱うかや、戻り値の型をどうするかによって、使用すべき関数や記述方法は異なります。

C++には古くからある標準ライブラリの関数から、C++11以降で標準化された便利な関数、そして型システムの特性を利用したキャストによる方法まで、複数の選択肢が存在します。

これらを正しく使い分けないと、計算精度の低下や、特定の条件下での意図しない挙動（バグ）を招く恐れがあります。

本記事では、std::floor、std::trunc、およびキャストによる切り捨ての違いを詳細に解説し、実務で役立つ具体的なコード例と共に紹介します。

目次 [ close ]
  1. 浮動小数点数の切り捨てにおける基礎知識
  2. floor関数の詳細と負の数値の挙動
    1. floor関数の特徴
    2. floor関数のサンプルコード
  3. trunc関数の詳細とゼロ方向への丸め
    1. trunc関数の特徴
    2. trunc関数のサンプルコード
  4. 型キャストによる切り捨てのメカニズム
    1. キャストによる切り捨ての特徴
    2. キャストのサンプルコード
  5. floor・trunc・キャストの比較まとめ
  6. 特定の桁数で切り捨てる方法
    1. 桁数指定切り捨てのロジック
    2. 任意の桁数での切り捨てサンプルコード
    3. 注意点：浮動小数点数の精度問題
  7. C++における丸めモードの制御
  8. 高度なテクニック：std::modf による整数部と小数部の分離
  9. まとめ

浮動小数点数の切り捨てにおける基礎知識

C++で数値を扱う際、まず理解しておくべきは「切り捨て」という言葉が持つ複数の意味です。

数学的な定義と、プログラミングにおける直感的な動作には時として乖離が生じます。

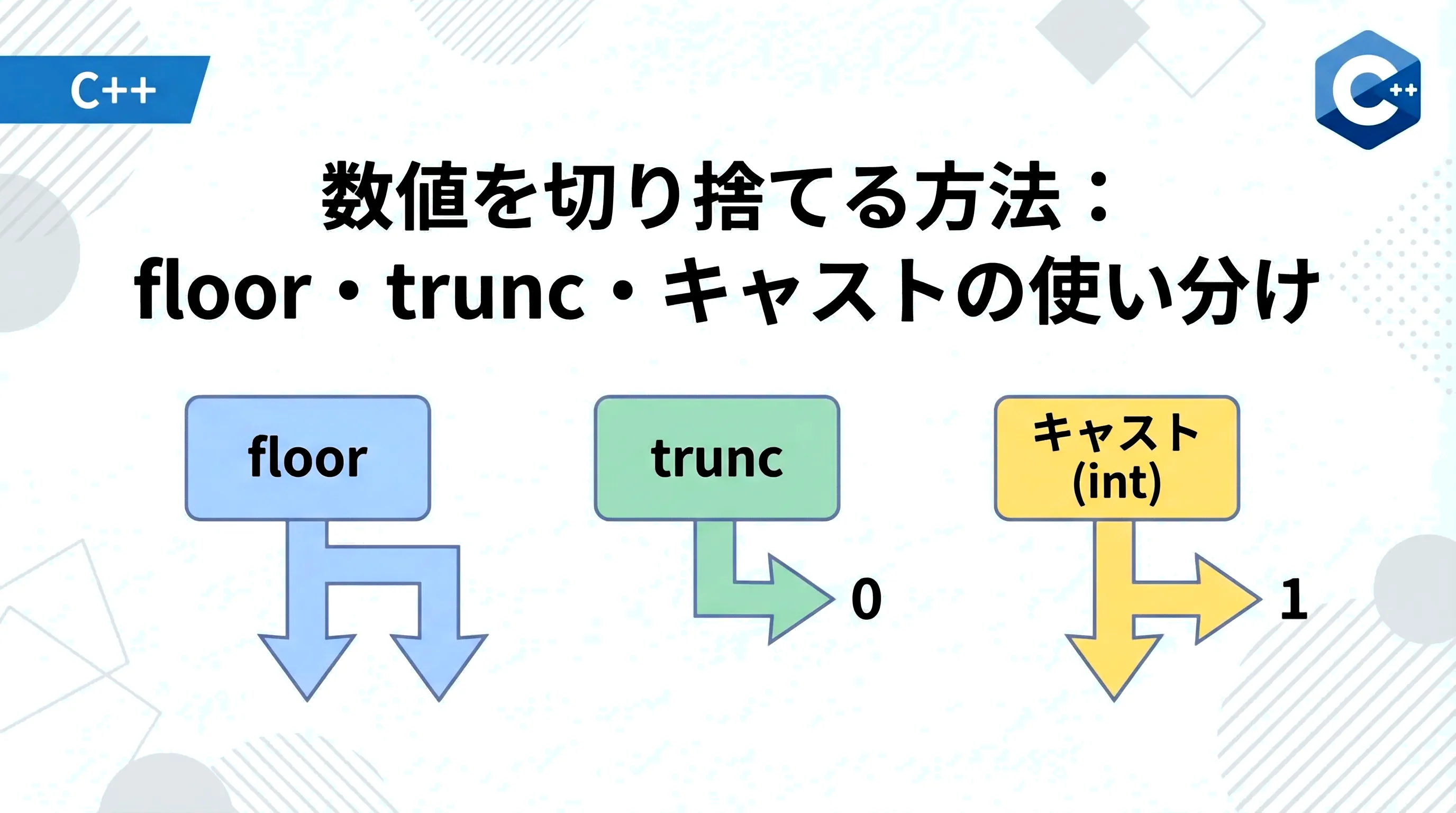
一般的にC++で「切り捨て」を実現する手法には、以下の3つのアプローチがあります。

  1. 床関数（floor）：その数値を超えない最大の整数を求める。
  2. ゼロ方向への丸め（truncation）：小数点以下を単純に除去し、ゼロに近い方の整数へ向かう。
  3. 整数型へのキャスト：変数自体の型を強制的に変換することで端数を捨てる。

これらの違いが最も顕著に現れるのは、負の値を処理する場合です。

例えば、-1.5を処理した際、-2.0になるのか-1.0になるのかは、選択した手法によって決まります。

まずはそれぞれの関数の仕様を深く掘り下げていきましょう。

floor関数の詳細と負の数値の挙動

std::floor関数は、ヘッダーファイル <cmath> で定義されている関数で、引数として与えられた数値 x に対して、x以下の最大の整数を返します。

これは数学で言うところのガウス記号に近い動作です。

floor関数の特徴

std::floorの最大の特徴は、数直線上で常に「左方向（負の無限大の方向）」に向かって数値を丸める点にあります。

正の数に対しては直感的な切り捨てとなりますが、負の数に対しては「値が小さくなる方向」に動くため注意が必要です。

  • 3 を floor すると 2.0 になる
  • -2.3 を floor すると -3.0 になる

このように、負の数において絶対値が大きくなる方向へ丸められるのが floor です。

座標系での計算や、タイマーのカウントダウン処理などで「常に現在の値を超えない範囲」を保証したい場合に適しています。

floor関数のサンプルコード

C++
#include <iostream>
#include <cmath> // std::floorを使用するために必要

int main() {
    double pos = 3.7;
    double neg = -3.7;

    // 正の数の切り捨て
    double res1 = std::floor(pos);
    // 負の数の切り捨て
    double res2 = std::floor(neg);

    std::cout << "floor(" << pos << ") = " << res1 << std::endl;
    std::cout << "floor(" << neg << ") = " << res2 << std::endl;

    return 0;
}
実行結果
floor(3.7) = 3
floor(-3.7) = -4

trunc関数の詳細とゼロ方向への丸め

std::trunc（truncate：切り詰める）関数は、C++11から導入された比較的新しい関数です。

この関数は、引数の小数点以下を単純に切り捨てる動作を行います。

trunc関数の特徴

std::truncは、正の数であっても負の数であっても、一貫して「ゼロに近い方の整数」へ丸めます。

数直線上で言えば、常に中央のゼロに向かって値が移動します。

  • 3 を trunc すると 2.0 になる
  • -2.3 を trunc すると -2.0 になる

多くのビジネスロジックや、単に「小数点以下は不要である」と考える一般的な文脈では、この std::trunc の挙動が最も期待に近いものとなるでしょう。

負の数の扱いにおいて floor と明確に異なるため、「負の無限大方向」なのか「ゼロ方向」なのかを常に意識する必要があります。

trunc関数のサンプルコード

C++
#include <iostream>
#include <cmath> // std::truncを使用するために必要

int main() {
    double pos = 3.7;
    double neg = -3.7;

    // truncによる切り捨て
    double res1 = std::trunc(pos);
    double res2 = std::trunc(neg);

    std::cout << "trunc(" << pos << ") = " << res1 << std::endl;
    std::cout << "trunc(" << neg << ") = " << res2 << std::endl;

    return 0;
}
実行結果
trunc(3.7) = 3
trunc(-3.7) = -3

型キャストによる切り捨てのメカニズム

C++において、浮動小数点数（doubleやfloat）を整数型（intやlong）にキャストすると、言語仕様として小数点以下が破棄されることが規定されています。

キャストによる切り捨ての特徴

この方法は関数呼び出しのオーバーヘッドがなく、最も高速に動作する傾向があります。

挙動としては std::trunc と同じく「ゼロ方向への切り捨て」が行われます。

ただし、いくつかの重要な注意点があります。

まず、戻り値が整数型になるため、元の値が整数型の最大値を超えている場合や、最小値を下回っている場合にはオーバーフロー（未定義動作の原因）が発生します。

また、非常に大きな浮動小数点数を扱う場合、精度が失われる可能性もあります。

C++では、古いCスタイルのキャスト (int)value よりも、意図を明確にする static_cast<int>(value) を使用することが推奨されます。

キャストのサンプルコード

C++
#include <iostream>

int main() {
    double val1 = 5.9;
    double val2 = -5.9;

    // static_castによる整数化（切り捨て）
    int i1 = static_cast<int>(val1);
    int i2 = static_cast<int>(val2);

    std::cout << "static_cast<int>(" << val1 << ") = " << i1 << std::endl;
    std::cout << "static_cast<int>(" << val2 << ") = " << i2 << std::endl;

    return 0;
}
実行結果
static_cast<int>(5.9) = 5
static_cast<int>(-5.9) = -5

floor・trunc・キャストの比較まとめ

それぞれの挙動の違いを理解するために、代表的な数値での処理結果を表にまとめました。

入力値std::floor (負の無限大へ)std::trunc (ゼロ方向へ)型キャスト (int)
2.82.02.02
2.12.02.02
-2.1-3.0-2.0-2
-2.8-3.0-2.0-2

使い分けの指針：

  • 数学的な低位境界を求めたい、あるいは常に小さい方の整数に丸めたい場合は std::floor を使用します。
  • 単に小数点以下を消去したい、または負の数でも「0.x」の部分だけを切り落としたい場合は std::trunc を使用します。
  • 結果をそのまま整数変数に代入したい、あるいはパフォーマンスが極めて重要な局面では static_cast を検討します（ただし、範囲チェックに注意）。

特定の桁数で切り捨てる方法

標準ライブラリの関数はすべて「整数値」への切り捨てを行います。

「小数点第2位まで残して切り捨てたい」といった、任意の桁数での処理は直接提供されていません。

このような場合は、10の累乗を掛けてから切り捨て、再び10の累乗で割るという手法をとるのが一般的です。

桁数指定切り捨てのロジック

例えば、3.14159 を小数点第2位で切り捨てて 3.14 にしたい場合、以下の手順を踏みます。

  1. 100（10の2乗）を掛けて 314.159 にする。
  2. std::floor または std::trunc を適用して 314.0 にする。
  3. 100 で割って 3.14 に戻す。

任意の桁数での切り捨てサンプルコード

C++
#include <iostream>
#include <cmath>
#include <iomanip>

/**
 任意の桁数で切り捨てる関数
 @param value 対象の数値
 @param precision 残したい小数点以下の桁数
 @return 切り捨て後の数値
 */
double custom_trunc(double value, int precision) {
    double pow_val = std::pow(10.0, precision);
    // truncを使用してゼロ方向へ切り捨て
    return std::trunc(value * pow_val) / pow_val;
}

int main() {
    double pi = 3.1415926535;

    std::cout << "Original: " << std::fixed << std::setprecision(10) << pi << std::endl;
    std::cout << "Trunc (2 digits): " << custom_trunc(pi, 2) << std::endl;
    std::cout << "Trunc (4 digits): " << custom_trunc(pi, 4) << std::endl;

    double neg_val = -3.1415926535;
    std::cout << "Original (neg): " << neg_val << std::endl;
    std::cout << "Trunc (neg, 2 digits): " << custom_trunc(neg_val, 2) << std::endl;

    return 0;
}
実行結果
Original: 3.1415926535
Trunc (2 digits): 3.1400000000
Trunc (4 digits): 3.1415000000
Original (neg): -3.1415926535
Trunc (neg, 2 digits): -3.1400000000

注意点：浮動小数点数の精度問題

上記の「10の累乗を掛ける」方法には、浮動小数点数特有の誤差という落とし穴があります。

コンピュータ内部では数値が2進数で表現されているため、10進数における 0.1 は無限小数となり、正確に表現できません。

そのため、計算過程で極めて小さな誤差（例：0.99999999999998 のような値）が発生し、切り捨てを行った結果、本来 1.0 になるべきところが 0.0 になってしまうといった現象が起こり得ます。

厳密な金融計算などを行う場合は、double型を直接操作するのではなく、整数型（最小単位を1として扱う「固定小数点数」方式）で管理するか、専用のデシマルライブラリを使用することを検討してください。

C++における丸めモードの制御

C++では、標準ライブラリの <cfenv> ヘッダーを使用することで、浮動小数点演算の「丸め方向」を環境レベルで制御することも可能です。

std::fesetround 関数を使用すると、プログラム全体の浮動小数点演算の挙動を変更できます。

  • FE_DOWNWARD：負の無限大方向（floor相当）
  • FE_TOWARDZERO：ゼロ方向（trunc相当）
  • FE_UPWARD：正の無限大方向（ceil相当）
  • FE_TONEAREST：最も近い値（round相当）

ただし、この方法はグローバルな状態を変更するため、予期せぬ場所で計算結果が変わってしまうリスクがあります。

現代的なC++開発においては、環境設定を変えるよりも、個別の場所で std::floor や std::trunc を明示的に呼び出す方が安全で可読性も高いとされています。

高度なテクニック：std::modf による整数部と小数部の分離

切り捨てそのものではありませんが、数値の「整数部分」と「小数部分」を同時に取得したい場合には std::modf が非常に便利です。

C++
#include <iostream>
#include <cmath>

int main() {
    double val = 123.456;
    double int_part;
    double frac_part = std::modf(val, &int_part);

    std::cout << "Original: " << val << std::endl;
    std::cout << "Integer Part: " << int_part << std::endl;
    std::cout << "Fractional Part: " << frac_part << std::endl;

    return 0;
}
実行結果
Original: 123.456
Integer Part: 123
Fractional Part: 0.456

この関数の戻り値（小数部）は、元の数値と同じ符号を持ちます。

整数部を取得する動作自体は std::trunc と同等ですが、小数部を後の計算で再利用したい場合に、計算による誤差を最小限に抑えつつ分離できるというメリットがあります。

まとめ

C++で数値を切り捨てる際は、まず「負の数をどのように処理したいか」を明確にすることが重要です。

  • 負の無限大方向へ丸めたい場合は、伝統的な std::floor を使用します。これは、常に元の数以下の最大の整数を得るための最も確実な方法です。
  • 単純に小数点以下を消去したい場合は、C++11で導入された std::trunc が最適です。正負にかかわらずゼロに向かって丸められるため、多くのビジネスロジックに適しています。
  • パフォーマンスを最優先し、結果を整数型で得たい場合は、static_cast<int> による型変換を利用します。ただし、値の範囲（オーバーフロー）には十分に注意を払う必要があります。

また、任意の桁数での切り捨てを行う際には、浮動小数点数の精度誤差（イプシロン）の問題が常に付きまといます。

より厳密な精度が求められるアプリケーションでは、10進数表現が可能なライブラリの使用や、整数を用いた固定小数点演算への切り替えも視野に入れてください。

それぞれの特性を理解し、適切に使い分けることで、バグの少ない堅牢な数値計算プログラムを構築することができるようになります。

本記事で紹介した使い分けを参考に、用途に最適な「切り捨て」を選択してください。