C言語におけるプログラミングでは、メモリやハードウェアを直接制御するために「ビット演算」が頻繁に活用されます。

その中でも、ビット反転演算子である チルダ (~) は、データの特定のビットを入れ替えたり、ビットマスクを作成したりする際に非常に重要な役割を果たします。

しかし、計算結果が直感的な数値と異なったり、負の数の表現方法に戸惑ったりすることも少なくありません。

本記事では、ビット反転の基礎から、計算の仕組み、実務での応用例、そして注意すべきポイントまでを詳しく解説します。

目次 [ close ]
  1. ビット反転演算子（~）の基礎知識
    1. ビット反転の概念
  2. ビット反転の計算の仕組みと「2の補数」
    1. 1の補数と2の補数の違い
    2. 計算式の導出
  3. C言語でのビット反転の実装例
    1. 基本的なプログラム例
    2. unsigned型（符号なし）での動作
  4. ビット反転の応用テクニック
    1. 1. 特定のビットをオフにする (ビットクリア)
    2. 2. 全ビットが1の値を生成する
  5. ビット反転を使用する際の注意点
    1. 整数昇格 (Integer Promotion) の影響
    2. 符号付き整数に対するシフトと反転
    3. 演算子の優先順位
  6. 実践：ビット反転を用いたデータ処理
  7. まとめ

ビット反転演算子（~）の基礎知識

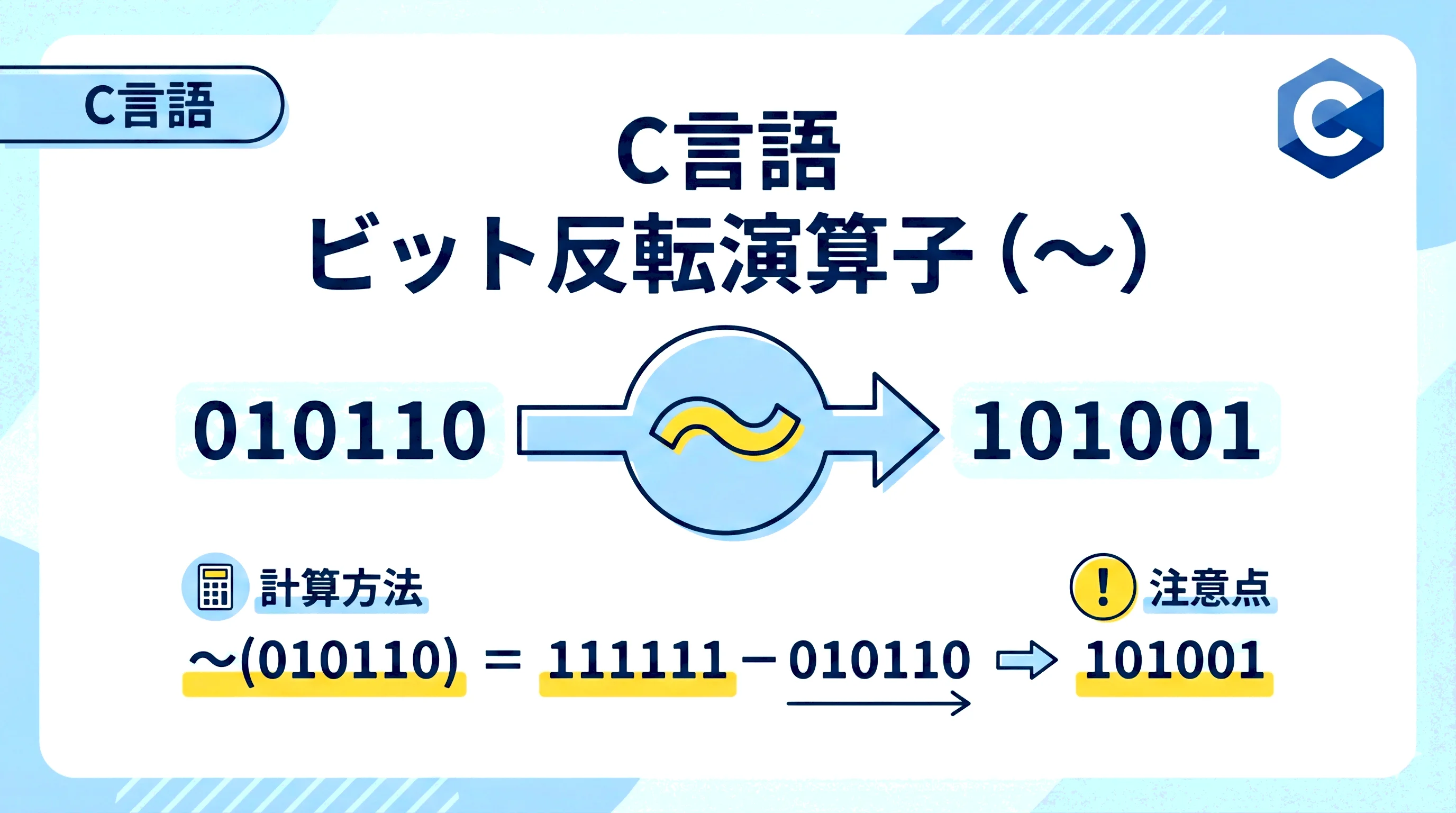
C言語におけるビット反転演算子 ~ は、単項演算子の一つであり、対象となる数値の全ビットを 0から1へ、1から0へ 置き換える操作を行います。

この操作は「1の補数」を求めることと同義であり、論理演算における NOT 演算に相当します。

ビット反転の概念

コンピュータの内部では、すべてのデータは 0 と 1 の組み合わせ（2進数）で保持されています。

ビット反転は、このビット列をそのまま反転させる単純な論理操作です。

例えば、8ビットの整数値がある場合、以下のように変換されます。

  • 元の値： 00001010 (10進数で10)
  • 反転後： 11110101 (10進数で-11 ※符号付きの場合)

このように、ビットそのものを反転させることは単純ですが、C言語のプログラム上で実行した際の結果（10進数での値）を理解するには、コンピュータにおける 負の数の表現形式 を知る必要があります。

ビット反転の計算の仕組みと「2の補数」

ビット反転を行った結果、なぜ期待した数値と異なる負の値が表示されるのか、その理由はC言語（および多くの現代的なCPU）が負の数を 「2の補数」 形式で表現しているためです。

1の補数と2の補数の違い

ビット反転演算子 ~ が行うのは「1の補数」を求める操作です。

一方で、私たちが通常扱う「負の数」は「2の補数」で定義されています。

  1. 1の補数：純粋にビットを反転させたもの。
  2. 2の補数：1の補数に「1」を加えたもの。

この関係性から、ある整数 x に対してビット反転を行うと、結果は -(x + 1) になります。

10進数2進数 (8ビット)ビット反転 (1の補数)10進数としての結果
00000000011111111-1
10000000111111110-2
50000010111111010-6
1270111111110000000-128

計算式の導出

なぜ ~x が -(x + 1) になるのかを考えてみましょう。

2の補数の定義では、負の数 -x は ~x + 1 と表されます。

この式を変形すると以下のようになります。

-x = ~x + 1 ~x = -x - 1 ~x = -(x + 1)

この数式は、符号付き整数 (signed int) を扱う際に非常に重要です。

ビット反転を行った結果を10進数で出力したときに「値が1ずれてマイナスになる」のは、この仕様に基づいています。

C言語でのビット反転の実装例

それでは、実際にC言語のプログラムでビット反転の挙動を確認してみましょう。

符号付き型 (signed) と符号なし型 (unsigned) では、表示される結果の解釈が異なります。

基本的なプログラム例

以下のコードは、整数値をビット反転させ、その結果を10進数と16進数で表示するものです。

C言語
#include <stdio.h>

int main() {
    int val = 10;
    int inverted_val = ~val;

    printf("元の値 (10進数): %d\n", val);
    printf("反転後の値 (10進数): %d\n", inverted_val);
    printf("反転後の値 (16進数): %x\n", inverted_val);

    return 0;
}
実行結果
元の値 (10進数): 10
反転後の値 (10進数): -11
反転後の値 (16進数): fffffff5

この結果から、10 を反転させると -(10 + 1) である -11 になっていることが確認できます。

また、16進数表示では上位ビットがすべて f になっており、広範囲のビットが反転していることがわかります。

unsigned型（符号なし）での動作

ビット演算を行う際は、通常 unsigned型 を使用することが推奨されます。

符号ビットの挙動に惑わされず、純粋なビット列として操作できるためです。

C言語
#include <stdio.h>

int main() {
    unsigned int u_val = 10;
    unsigned int u_inverted = ~u_val;

    printf("符号なし元の値: %u\n", u_val);
    // 32ビット環境を想定
    printf("符号なし反転後: %u\n", u_inverted);
    printf("符号なし反転後 (16進数): 0x%08x\n", u_inverted);

    return 0;
}
実行結果
符号なし元の値: 10
符号なし反転後: 4294967285
符号なし反転後 (16進数): 0xfffffff5

符号なし型の場合、負の数という概念がないため、反転したビット列がそのまま巨大な正の整数として解釈されます。

ビット反転の応用テクニック

ビット反転演算子は、単独で使用するよりも、他のビット演算子（AND, OR, XOR）と組み合わせて使用することで、その真価を発揮します。

1. 特定のビットをオフにする (ビットクリア)

特定のフラグ（ビット）だけを 0 にし、他のビットを保持したい場合、ビット反転と AND演算 (&) を組み合わせます。

例えば、00001000 (第3ビット) だけをオフにしたい場合、まずそのビットだけが立っている値を用意し、それを反転させて「そのビットだけが0のマスク」を作ります。

C言語
#include <stdio.h>

#define FLAG_A (1 << 0) // 00000001
#define FLAG_B (1 << 1) // 00000010
#define FLAG_C (1 << 2) // 00000100

int main() {
    unsigned char status = FLAG_A | FLAG_B | FLAG_C; // 00000111
    printf("初期状態: 0x%02x\n", status);

    // FLAG_B だけをクリアする
    // ~FLAG_B は 11111101 となる
    status = status & ~FLAG_B;

    printf("FLAG_Bクリア後: 0x%02x\n", status); // 00000101 (FLAG_A | FLAG_C)

    return 0;
}
実行結果
初期状態: 0x07
FLAG_Bクリア後: 0x05

このように、status &= ~FLAG という記述は、デバイスドライバや組み込み開発において、特定の制御レジスタを操作する際の定番の書き方です。

2. 全ビットが1の値を生成する

移植性の高いコードを書く際、データの全ビットを 1 にしたいことがあります。

その場合、単純に ~0 と記述することで、型のサイズに依存せずに全ビットが立っている状態を作り出せます。

C言語
unsigned int mask = ~0U; // すべてのビットが1のunsigned int

これは、将来的にシステムのビット数が32ビットから64ビットに変わったとしても、正しく全ビットをカバーできるため、マジックナンバーを使用するよりも安全です。

ビット反転を使用する際の注意点

ビット反転は強力ですが、C言語特有の仕様による罠がいくつか存在します。

整数昇格 (Integer Promotion) の影響

C言語には、char や short などの小さな整数型に対して演算を行う際、一時的に int 型に拡張してから計算を行う「整数昇格」というルールがあります。

これがビット反転で意図しない挙動を引き起こすことがあります。

C言語
unsigned char a = 0x0F; // 00001111
unsigned char b = ~a;   // 11110000 を期待

このとき、~a の計算は int 型（通常32ビット）で行われるため、結果は 0xFFFFFFF0 となります。

これを再び unsigned char に代入すれば下位8ビットが切り出されて期待通り 0xF0 になりますが、比較演算などで直接使用すると予期せぬ結果を招く可能性があります。

注意： 小さい型に対してビット反転を行う場合は、結果を適切な型でキャストするか、マスク処理を行って上位ビットを切り捨てることが重要です。

符号付き整数に対するシフトと反転

符号付き整数に対してビット演算を行うことは、C言語の規格上、未定義動作や実装依存の動作を含むことがあります。

特に負の数に対するビット操作は、そのコンピュータがどのような負数表現を採用しているかに依存するため、ビット演算を行う変数は原則として unsigned 型として宣言すべき です。

演算子の優先順位

チルダ ~ 演算子は、加減算などの算術演算子よりも優先順位が高いという特徴があります。

優先順位演算子
高~ (ビット反転), ! (論理否定), ++, --
中*, /, %
低+, -

例えば、~x + 1 という式は、まず x が反転され、その後に 1 が加算されます。

括弧を適切に使用して、意図した順序で計算が行われるように注意しましょう。

実践：ビット反転を用いたデータ処理

ビット反転の応用として、簡単なチェックサムの計算や、データの特定パターン検出などで利用されることがあります。

以下の例では、データの補数を確認することで、簡易的なエラーチェックのような概念を再現します。

C言語
#include <stdio.h>

// データの正当性を確認する関数（簡易的な概念）
int is_complement(unsigned char original, unsigned char inverted) {
    // 元の値とその反転を足し合わせると、全ビットが1 (0xFF) になるはず
    return (unsigned char)(original + inverted) == 0xFF;
}

int main() {
    unsigned char data = 0x3A;        // 00111010
    unsigned char inv_data = ~data;   // 11000101

    printf("データ: 0x%02x, 反転データ: 0x%02x\n", data, inv_data);

    if (is_complement(data, inv_data)) {
        printf("整合性チェックOK: データは正しく反転されています。\n");
    } else {
        printf("整合性チェックNG: データが破損しています。\n");
    }

    return 0;
}
実行結果
データ: 0x3a, 反転データ: 0xc5
整合性チェックOK: データは正しく反転されています。

この性質（x + ~x は常に全ビットが 1 になる）は、ビット演算の理論を理解する上で非常に役立ちます。

まとめ

C言語におけるビット反転演算子 ~ は、単純にビットを入れ替えるだけの機能ですが、その背後にある 2の補数 の仕組みや 整数昇格 のルールを正しく理解していないと、バグの原因になりやすい要素でもあります。

本記事のポイントを振り返ります。

  • ビット反転は 0 を 1 に、1 を 0 に変換する操作。
  • 符号付き整数では ~x は -(x + 1) となる。
  • 特定のビットをクリア（オフ）にする際に & ~ の組み合わせで使用される。
  • ビット演算を行う際は、予期せぬ挙動を防ぐために unsigned 型を使用するのが鉄則。

これらの知識を身につけることで、レジスタ操作やパケット解析、フラグ管理といった低レイヤのプログラミングをより正確かつ効率的に行えるようになります。

C言語のビット演算をマスターして、より深いシステムプログラミングの世界に挑戦してみてください。